Masse
et poids (et notion de
force)
(1) LA MASSE.
La masse
de tout objet nous renseigne sur la
quantité de
matière constituant cet objet. Elle s'exprime en kilogramme
(kg)
ou multiples (tonne : t) ou sous-multiples ( gramme : g, milligramme :
mg ; etc).
masse d'un clou : 5
g
masse d'une
pomme : 100 g
masse d'un
bébé
: 4 kg
masse d'un
adulte : 65 kg
masse d'un
camion : 30 t
Par exemple, entre deux pommes, l'une de 80g et l'autre de 160 g, celle
qui contient donc le plus de matière (où
donc il y
a le plus à manger), c'est indépendamment du
volume, ou
de la taille, celle de 160g.
A noter : le mot masse est souvent associé (de par
le
vocabulaire courant, par des termes tels que massif, massue, une
masse à frapper), à une quantité « importante
». On
peut pourtant parler de masse d'un moustique, d'un
atome tout autant
que celle d’un éléphant ou
d’une enclume !
(2) LE POIDS.
Dans la vie courante, la notion de poids est
confondu avec la
notion de masse (on dit par exemple qu'on trouve son poids de 60 kg
trop important !). Or ces deux notions sont différentes.
Tous les objets, des plus petits aux plus gros,
situés
dans le voisinage d'une planète, telle que la Terre, sont
attirés par celle-ci, vers son centre : c'est le
phénomène d'attraction universelle,
découvert et
formalisé par Newton. (d'où la pomme en clin
d'œil...)
Cette attraction planétaire est
désignée
plus souvent par les physiciens sous le nom de pesanteur.
Le terme
de
poids
étant le plus souvent réservé au cas
où la planète en question est la Terre ; (mais
rien
n'empêcherait de parler de poids lunaire, de poids martien,
etc..)
Le poids
d'un objet est donc une force,
toujours dirigée
localement selon la verticale, vers le bas. (Direction d'un fil
à plomb: le poids du plomb est responsable du fait que le
fil
est tendu, selon la verticale.)
(3) QU’EST QU’UNE FORCE ?
Là encore, le vocabulaire de la vie de tous les jours est
flou
(« manquer de forces », « ce gars
là, quelle
force ! », …).
Plus précisément, une force
est une action
mécanique pouvant déformer un objet
ou bien modifier (ou
créer) un mouvement. Les physiciens la modélisent
par un
vecteur (représenté par une flèche et
noté
en gras), qui réunit les caractéristiques de
cette force
: direction et sens, valeur numérique (intensité)
qui
s’exprime en Newton (N) (en hommage justement au physicien
anglais
), et point d’application.
Pour notre pomme, le poids
sera donc représenté par
une flèche verticale P,
vers le bas, appliquée en un point appelé centre
de
gravité.
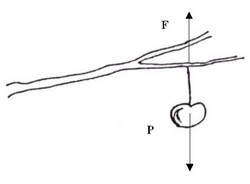
La
pomme étant immobile
sur l’arbre, il est nécessaire de faire
intervenir une 2eme force
F
(exercée par la branche sur la tige) qui
compense le poids, sinon…
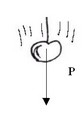
…c’est la mise en mouvement : chute !
(4) QUAND LES NOTIONS DE POIDS ET
DE MASSE SE REJOIGNENT...
Si nous résumons pour l'instant : la
masse d'un objet
mesure la quantité de matière tandis que son
poids est
une force, exercée par la Terre sur cet objet.
Mais il est facile de comprendre que le poids de l'objet est
d'autant plus grand que la masse de l'objet augmente. En d'autres
termes l'attraction exercée par la Terre sur l'objet
augmente au
fur et à mesure que la quantité de
matière
contenue dans cet objet augmente. Par exemple, le poids d'un moustique
est plus petit que celui d'un éléphant, car leurs
masses
sont différentes ! Masse et poids sont deux
quantités proportionnelles.
Si la masse d'un
objet double,
son poids double
également. Le poids
(l'intensité de l'attraction terrestre) d'un objet de masse
m
exprimée en kg est donné par la relation de
proportionnalité P = m * g où g est un coefficient de proportionnalité
valant sur
Terre à peu près 10 ( 9,81 exactement) et
appelé
intensité de la pesanteur.
Par exemple le poids de la pomme de 80 g est de 0.08 x 10 soit 0,8 N.
Le poids de la pomme de 160 g est de 1,6 N. (Sur le schéma
n’ont
été notées que les masses)
Dans la mesure où les deux
valeurs de masse et de poids sont proportionnelles, on comprend
pourquoi il est si peu souvent fait de distinction dans la vie de tous
les jours. Exprimer l'une revient à exprimer l'autre. Si on
pouvait changer de planète, la différence
apparaîtrait mieux, car si la masse d'un objet ne change pas
(
sauf si on croque dans la pomme!), l'attraction exercée par
la planète peut, elle, changer. Ainsi, sur la Lune, le
coefficient
g vaut 1,6 seulement. Un objet de poids 100 N sur la Terre (donc de
masse 10 kg) a un poids lunaire de 16 N, six fois plus petit.
Les astronautes pouvaient emmener un très lourd équipement
(scaphandre, réserves d'air…) sans
inconvénient. Ou tenter des records de saut en hauteur (quoique le
scaphandre est peu
souple et la fantaisie peu de mise lors de ces missions : lire
plutôt les aventures de Tintin sur la Lune, où les
phénomènes sont décrits presque
toujours avec
rigueur scientifique).
(5) ET DANS
L'ESPACE ?
La masse n'est évidemment pas modifiée.
Par contre
le poids ira diminuant au fur et à mesure qu'on
s'éloigne
de la Terre, mais il ne s'annulera jamais, sauf dans le cas limite
où on se trouve infiniment loin de la Terre.
Voici un petit tableau donnant pour un objet de masse 10 kg
l'intensité de son poids (intensité de
l'attraction
terrestre) pour quelques altitudes.
Altitude
|
0
(niveau de la mer)
|
100
km
|
1000
km
|
10 000
km
|
Poids
|
98 N
|
95 N
|
72 N
|
15 N
|
L'atmosphère finit vers 200 km. Vous constatez qu'au dessus, dans le
vide de l'espace, le poids n'est ni nul, ni
même négligeable : la présence ou l'absence d'air n'a en effet aucun
lien avec l'attraction planétaire ; ce sont deux
choses distinctes.
Les phénomènes dits
d'apesanteur (ou d'impesanteur,
pour éviter des confusions
à l'oral) pour lesquels l'attraction planétaire semble nulle sont
assez
délicats à expliquer. Disons seulement que leur
cause
n'est pas une absence d'attraction (la majorité des orbites
des
satellites ou de la navette se situe entre 200 et 1000 km,
où
l'attraction terrestre est encore très forte, voir le
tableau) ;
en deux mots, ce phénomène d'impesanteur provient
du
mouvement du vaisseau :

|

|
Dans
la navette spatiale en orbite
|
Dans
un avion d'entrainement terrestre en chute parabolique (avion
ZéroG du CNES)
|
(6) LA MESURE DES MASSES OU DES POIDS (LES BALANCES).
Il existe en gros deux types de balances : Celles qui mesurent
directement un poids, d'après la
déformation plus ou moins importante d'un ressort, comme par
exemple le pèse-personne, ou pour les balances plus modernes
(électroniques) la déformation d'une "jauge de
contrainte". Le constructeur gradue directement en kg, car poids et
masse sont proportionnels ; ce type de balance donnerait des
indications erronées sur une autre planète, par
exemple
la Lune.
Celles qui comparent des masses, comme par exemple la balance
Robertval, ou qui sont basées sur le déplacement
d'une masselotte (pèse-lettres) : il y a équilibre si les masses posées
sur les plateaux sont égales : cela
nécessite donc l'utilisation de masses marquées,(qu'on appelle
d'ailleurs improprement poids !). Comme ces balances
fonctionnent par comparaison de masses, elles donneraient aussi des
indications correctes ailleurs que sur Terre.
(7) LES
EQUILIBRES.
Dans les situations de classe, on travaille souvent cette notion par
des manipulations faisant intervenir des objets assez lourds
(écrous, pièces de monnaie, pinces à
linge), qu’on
dispose sur une barre pouvant tourner autour d’un point fixe.
En fait, même si les élèves comptent les objets
fixés ou lisent leur masse, lors de ces manipulations, on
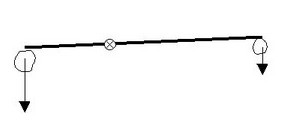
compare (et on trouvera une relation entre ) des poids : si on place
deux pinces à gauche et une pince à droite, cela
revient
à avoir un poids double à gauche.
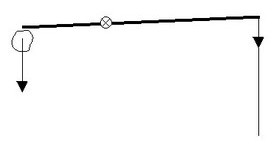
Cette précision est utile
lorsqu’on réfléchira au fonctionnement
du levier. En
effet dans ce cas, on essaie de soulever un objet lourd, en
exerçant justement une force F qu’on veut la plus
faible
possible (pour se fatiguer le moins possible !).
(8) EN
CONCLUSION...
Ces distinctions, subtiles, n'ont pas à
être
abordées à l'école
élémentaire. On
pourra parler indifféremment de poids d'un objet pour
désigner sa masse, de dire peser à la place de
mesurer la
masse. La différentiation n’a
d’opportunité que lors de
phénomènes « exotiques » (en
astronautique).
Par contre on pourra désigner correctement : " la
boite de
masses marquées ", objet d’ailleurs de
plus en plus rare
dans notre quotidien.
Quelques
petites questions pour finir :
-1- Calculer votre poids.
-2- Quand vous achetez
un filet de
pommes de terre, qu'est-ce qui vous importe, le poids ou la masse du
filet?
-3- A la Cité
des Sciences et
Techniques de la Villette à Paris, il y a 3
pèse-personnes, l'un prévu pour fonctionner sur
la Terre,
l'autre sur la Lune, le dernier sur Mars. Ils sont gradués
en
kg. Vous montez sur chacun d'eux. Que doivent-ils indiquer?
-4- Cela a-t-il un sens
de parler du
poids de la Terre?